סולמות סטטיסטיקה
חזרה לכלל החומרים
תודה לג'ני דימנקו
חלק
א: סולמות מדידה
סטטיסטיקה היא למעשה כלי עזר למחקר. ישנה תופעה שמעניינת אתנו ואנו רוצים לחקור אותה. לשם כך, אנו צריכים לאסוף נתונים, ובאמצעות הסטטיסטיקה אנו בוחנים את הנתונים.
דוגמה 1: פעם נתנו לי טיפ לשמור את הבצל במקרר כדי שלא אדמע. האם זה נכון?
לשם כך אני יכולה לאסוף אנשים שיחתכו בצל שנשמר במקרר ואנשים שיחתכו בצל שנשמר מחוץ למקרר ולבחון מהו הקשר בין אופן שימור הבצל ולדמוע (מתאם קרמר אותו נלמד בהמשך).
דוגמה 2: יש המתרצים שהמרחק יפריע בקשר הזוגי. האם זה נכון עם כל הטכנולוגיה שיש היום? אפשר למשל לבחון האם חברות בין אנשים ממקומות רחוקים בארץ קצרה יותר מחברות בין אנשים הגרים קרוב.
כדי לאסוף נתונים אנחנו צריכים למצוא דרך לייצג את התופעה ובד"כ הייצוג הינו ייצוג מספרי. לפיכך כל תופעה ננסה לקודד למספרים, לדוגמה: חום מתורגם למעלות צלזיוס או פרנהייט. חרדה תימדד למשל על ידי רמת מוליכות העור, מספר ציפורניים שנקססו וכו'.
את המיפוי
של תופעה למספרים ניתן לבצע במספר דרכים
� את הדרכים השונות מייצגים סולמות מדידה
שונים: שמי, סדר, רווח ומנה (מהפשוט למורכב).
סולם שמי:
המיפוי למספר מאפשר זיהוי בלבד של הערך. החוק המנחה במיפוי קטגוריות בתופעה למספר:
1. לא ניתן מספר זהה לשני דברים שונים.
2. לא ניתן מספר שונה לשני דברים זהים.
דוגמה: ברקוד של מוצר בסופר. הקלדת המספר בקופה נותנת את שם המוצר, מספר קוד אחר פירושו מוצר אחר. ולכן מלבד זהות, למספר אין כל משמעות.
גם במחקר על הבצל נקודד את התנאים "בצל מהמקרר" כ- 1 ו"בצל מחוץ למקרר" כ- 2. למספרים אלו אין שום משמעות מלבד המיקום בו נשמר הבצל.
הגדרה: טרנספורמציה � פעולה חשבונית המשנה את המספר � חיבור חיסור כפל או חילוק עם מספר מסוים.
טרנספורמציה מותרת על מספרים בסולם שמי - כל טרנספורמציה שתשמור על הזהות. פעולה שתגרום שוויון בין שני מספרים שונים בסולם אסורה! למשל: מותר לכפול ב- 2 אך לא ב- 0.
לא ניתן להשמיט את הספרה האחרונה של הקודים 35 ו 39 כי שני דברים שונים יהפכו לבעלי קוד זהה (לספרה 3) והזהות לא תישמר.
מדדים
סטטיסטים מותרים לחישוב - רק שכיח (למשל:
מאיזה קוד מוצר יש הכי הרבה מוצרים כאלו
על המדף, או שכיחות בנים ובנות בכיתה). אין
משמעות לממוצע או חציון של קודים או של
זכר ונקבה.
סולם סדר:
מיפוי תופעה שיש בה היררכיה (סדר), אך אין משמעות למרווחים בין המספרים.
כל מספר בסולם מהווה תווית זיהוי של קטגוריה בתופעה ובנוסף ניתן לסדר את המספרים באופן היררכי. ניתן להבחין בסדר היררכי בקטגוריות בתופעה והמספרים המייצגים את הקטגוריות ייצגו גם את הסדר ההיררכי בניהן. עם זאת בסולם זה אין משמעות למרווחים בין המספרים בסולם. לא ניתן להגיד "בכמה" מספר אחד גדול מהשני.
דוגמה: מחקר על תהליך האבולוציה ידרג את השלבים השונים. קוף יקבל מס' 1, האדם הקדמון 2, והאדם המודרני 3. המספרים מייצגים את הסדר ההיררכי באבולוציה אך הם לא מייצגים כמה האדם הקדמון מתקדם יותר מן הקוף או האם המרחק בין הקוף לאדם הקדמון זהה למרחק בין האדם הקדמון לאדם המודרני.
חשוב: סקאלה סובייקטיבית עם 4 רמות תהיה סולם סדר, סקאלה סובייקטיבית עם 5 רמות ומעלה תהיה סולם רווח
טרנספורמציה מותרת על מספרים בסולם סדר - כל טרנספורמציה ששומרת על הזהות והסדר ההיררכי. אפשר למשל לכפול או לחלק ב- 2 אבל לא ב- (2-), או כל מספר שלילי אחר.
מדדים
סטטיסטים מותרים לחישוב - אם יש לנו התפלגות
שכיחויות בסולם סדר, ניתן לחשב שכיח, חציון,
טווח בין רבעוני ומאונים.
סולם רווח
בסולם זה בנוסף לזהות ולסדר קיימת משמעות למרווחים בין המספרים בסולם. ההפרש בין המספרים בסולם מייצג את ההפרש בין הקטגוריות בתופעה ולכן יש למרווחים משמעות.
לפיכך, קטגוריה שהמיפוי שלה למספר הוא 61 גדולה ביחידת מידה אחת מקטגוריה שהמיפוי שלה הוא 60 וההפרש בניהם זהה להפרש בין קטגוריה שהמיפוי שלה הוא 231 לבין קטגוריה שהמיפוי שלה הוא 230.
לדוגמא: מעלות טמפרטורה.
טרנספורמציה מותרת על מספרים בסולם רווח - טרנספורמציה ליניארית חיובית בלבד. כלומר, עבור כל הערכים ובאותה מידה נבצע חיבור או חיסור של מספר קבוע ו/או הכפלה בקבוע חיובי בלבד. הכפלה במספר שלילי הופכת את הסדר. (b>0) y=bx+a
טרנספורמציה זו שומרת על רווחים קבועים בין המספרים וכן על זהות וסדר.
מדדים
סטטיסטים מותרים לחישוב: כולם. למשל:
שכיח, חציון, טווח בין רבעוני ומאונים, ממוצע,
שונות, סטיית תקן, ציוני תקן וכו'.
משמעות האפס בסולמות שמי, סדר ורווח: נקודת האפס נקבעת באופן שרירותי. המשמעות של אפס איננה "כלום" או העדר מוחלט של תופעה. לכן, בכל הסולמות האלו 30 זה לא פי 3 מ 10.
לדוגמה:
במיפוי קווי אורך ורוחב של כדור הארץ קו
המשווה נקבע שרירותית כאפס. קו האפס יכול
היה להיות במקום אחר. או למשל: 0 מעלות חום
אין פירושו שאין חום.
סולם מנה:
בסולם זה בנוסף לזהות לסדר ולמרווחים בין המספרים ישנה משמעות ליחס בין המספרים והאפס מוחלט. כלומר האפס אינו נקבע שרירותית אלא מייצג "כלום" מהתופעה, העדר מוחלט של התופעה.לכן בסולם זה 30 זה בדיוק פי 3 מ 10.
דוגמה: אחוז רייטינג לתוכנית טלוויזיה. 0% פירושו כי אין צופים לתוכנית.
טרנספורמציה מותרת על מספרים בסולם מנה - מכפלה בקבוע חיובי בלבד. כלומר, עבור כל הערכים נבצע הכפלה מספר קבוע חיובי. y=bx , b>0.
טרנספורמציה זו שומרת על היחסים, על רווחים קבועים בין המספרים וכן על זהות וסדר. אם נוסיף או נחסיר מספר קבוע היחס בין המספרים לא נשמר. אם נכפיל במספר שלילי הסדר יתהפך.
מדוע אי אפשר להוסיף/להחסיר קבוע? נניח שהסולם שלי הוא 2-4-8 ישנו יחס פי 2 בין אחד לשני. אבל אם נוסיף 1 לכל הערכים הם יהיו 3-5-9. לאחר ההוספה היחס לא נשמר 9 הוא לא פי 2 מ-5 ו-5 אינו פי 2 מ-3.
מדדים
סטטיסטים מותרים לחישוב - כולם.
טבלה מסכמת:
| סוג המדידה | תכונה | טרנספורמציה מותרת | מדדים
סטטיסטיים לחישוב | |||
| זהות | סדר | הפרש | יחס
ואפס מוחלט | |||
| סולם
שמי
(נומינלי) |
+ | - | - | - | שומרת זהות | שכיח |
| סולם
סדר
(אורדינלי) |
+ | + | - | - | חיסור, חיבור הכפלה בחיובי | שכיח, חציון, טווח בין רבעוני ומאונים |
| סולם
רווח
(אינטרוול) |
+ | + | + | - | חיסור, חיבור הכפלה בחיובי | כולם |
| סולם
מנה
(יחס) |
+ | + | + | + | הכפלה ב חיובי | כולם |
כיצד
נדע מהו הסולם? נתחיל מהגבוה לנמוך על-ידי
אלימינציה (שלילה): קודם נשאל "האם האפס
מייצג כלום?" אם לא, אזי זה לא מנה, ואז
נשאל האם יש משמעות לרווחים... וכך הלאה.
תרגיל 1: סולמות
קבעו מה הסולם המתאים בכל אחד מהמקרים הבאים:
- שעות בשעון - רווח
- קומות בקניון עזריאלי (קומה 2, קומה 1, קומה 0 (כניסה), חניון 1-, חניון 2-...) - רווח
- קידוד 1=אוהב, 2=שונא, 3=אדיש � שמי כי אין משמעות לסדר
- מספר חיילים שקיבלו צו 8 במלחמת לבנון השנייה � מנה
- חום תנור אפייה � רווח
- זווית במעלות של מצולע - מנה
חלק ב: התפלגות שכיחויות
� טבלאות וגרפים
מורות תמיד מתנגדות לשיעורי דשא בטענה כי במקום ללמוד בשיעור התלמידים יתעסקו בדברים שוליים. האם אכן שיעורי דשא יעילים פחות משיעורים בכיתה? הנה יש לפנינו שאלת מחקר, אותה נבחן בניסוי פשוט. אנו יודעים מה ממוצע הציונים של סטודנטים הלומדים בכיתות (ממוצע האוכלוסייה). כדי לבחון את שאלתנו, נלמד קבוצת סטודנטים בדשא שברחבת הקמפוס ונבחן על החומר הנלמד. בתום הרצת הניסוי יש לנו אוסף ציונים ואנו רוצים לבחון האם ציונים אלו נמוכים מהציונים הידועים באוכלוסיה.
מטרת
הסטטיסטיקה התיאורית היא לתת תיאור ברור
ופשוט של אוסף גדול של נתונים. על מנת שנוכל
ללמוד, לפרש או להסיק מהנתונים מידע כלשהו,
ראשית עלינו לארגן את הנתונים. בשיעור הנוכחי
נלמד כיצד לעשות זאת באמצעות התפלגות שכיחויות
המוצגת בטבלת שכיחויות או גרפים.
שכיחות - מסומנת f(x) מהמילה � frequency ופירושה, כמה תצפיות בעלות ערך מסוים, או כמה תצפיות בטווח ערכי הקטגוריה.
התפלגות
שכיחויות: התפלגות השכיחויות מלמדת אותנו
איך השכיחות מתפזרת בתופעה. למשל, האם יש
לי הרבה יותר ציונים גבוהים, נמוכים וכו'.
ניתן להראות את התפלגות השכיחויות בטבלאות
או גרפים
אופן ההצגה (איזו טבלה או איזה גרף) תלוי האם המשתנה בדיד או משתנה רציף
משתנה רציף: משתנה שיכול תיאורטית לקבל אין ספור ערכים בין 2 ערכים (ציר מספרים רציף). דוגמא: טמפרטורה
משתנה
בדיד: משתנה שיכול לקבל מספר סופי של
ערכים (ציר מספרים לא רציף, אלא בקפיצות).
דוגמא: מידת נעליים.
משתנה בסולם שמי או סדר - הוא בהכרח בדיד !
לעומת
זאת, משתנה בסולם רווח או מנה - זה תלוי ויש
לבחון האם הוא מקוטע או לא.
2 דרכים להציג את הנתונים: טבלת שכיחויות או גרף
I הצגה בטבלת שכיחויות
II הצגה גראפית
טבלת שכיחויות עבור משתנה רציף � טבלה עם קטגוריות רציפות
ערכי המשתנה (הציונים במבחנים) מיוצגים בקבוצות מוציאות וממצות ביחס לשכיחותן. כלומר, הקטגוריות צריכות להיות:
1. מוציאות - ערך מסוים של משתנה לא יופיע בשתי קבוצות.
2. ממצות - לכל ערך אפשרי של המשתנה יהיה מקום.
לכל תצפית מקום באחת מהקטגוריות ובמקום אחד בלבד.
למשל, אם אנחנו מגדירים:
40-50 � נכשל
50-60 � עבר
65-75 � בינוני
76-85 � טוב
86-100 � טוב מאוד
קיבלנו
קבוצות שאינן ממצות (כי אדם שקיבל 64, אינו
שייך לשום קבוצה) ואינן מוציאות (משום שאדם
שקיבל 50 יכול להשתייך לשתי קבוצות: כנכשל
ועבר).
מושגים וחישובים לגבי טבלת שכיחויות עם קטגוריות רציפות:
1.
רוחב הקטגוריה - מגדיר את גודל הקטגוריה
ונותן מידע על אופן קיבוץ הנתונים (עד כמה
פישטנו את הנתונים). מחושב ע"י ההפרש
בין הגבולות (ראה בטבלה בעמודת רוחב הקטגוריה
את החישוב בקטגוריה השנייה מלמטה). במקרים
רבים רוחב הקטגוריה אינו קבוע.
2.
צפיפות � שכיחות האנשים בקטגוריה ביחס
לרוחב הקטגוריה. ככל שיש יותר אנשים והקטגוריה
קטנה יותר, קטגוריה זו צפופה יותר. ככל שקטגוריה
צפופה יותר, כך הערכים בה יהיו פחות שונים,
כי יש פחות אופציות לערכים.
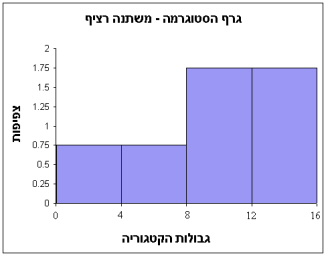
| צפיפות
D=f(x)/i |
רוחב
קטגוריה
i |
שכיחות
f(x) |
גבולות קטגוריה |
| 0.75 | 4 | 3 | 0-4 |
| 0.75 | 4 | 3 | 4-8 |
| 1.75 | 4 | 7 | 8-12 |
| 1.75 | 4 | 7 | 12-16 |
גרף היסטוגרמה � גרף למשתנה רציף: שכיחות מיוצגת בשטח
מתי נשתמש בהיסטוגרמה? מתאימה להצגת נתוני משתנה רציף המקובץ לקטגוריות רציפות.
ציר ה � X : גבולות הקטגוריה. ציר Y : הצפיפות.
תחילה
יש לסמן גבולות על ציר ה- X ולצייר ציר Y עם
ערכי הצפיפות. כעת, עבור כל קטגוריה נמתח
קו כלפי מעלה מגבול עליון וגבול תחתון עד
גובה הצפיפות של אותה קטגוריה, ונקבל ריבוע.
שטח הריבוע שווה לשכיחות של אותה קטגוריה
ולכן שכיחות מיוצגת בשטח.
טבלת שכיחויות עבור משתנה בדיד
דוגמה לטבלה שערכיה מספריים
דוגמה לטבלה שערכיה מילוליים (סולם סדר)
| שכיחות
f(x) |
מידת עישון |
| 3 | לא מעשן כלל |
| 7 | מעשן מעט |
| 9 | מעשן הרבה |
| 5 | מעשן כבד |
דוגמה לטבלה שערכיה מילוליים (סולם שמי)
| שכיחות
f(x) |
פרי אהוב |
| 3 | מנגו |
| 7 | בננה |
| 9 | מלון |
| 5 | אבטיח |
דיאגראמת מקלות � גרף למשתנה בדיד: שכיחות מיוצגת בגובה
מתי ואיך נשתמש בדיאגראמת מקלות ?
אנו
נשתמש בגרף זה במידה והמשתנה בדיד (סולם
שמי או סולם סדר)
ציר ה-X : ערכי המשתנה האפשריים. ציר ה-Y: השכיחות.
לכל
מרכז קטגוריה (ערך בציר ה- x) נצייר מקל אנכי
בגובה השכיחות.
תרגיל 2: משתנה בדיד או רציף, גרף היסטוגרמה או מקלות?
לפניך רשימת משתנים. עבור כל אחד ציין האם הוא משתנה בדיד או רציף ומהו הגרף המתאים ביותר:
| משתנה | בדיד או רציף | הגרף המתאים ביותר |
| זמן טיסה | רציף | היסטוגרמה |
| מספר מטלות | בדיד | מקלות |
| שיעור השתתפות נשים בכוח עבודה | רציף | היסטוגרמה |
| חברת אופנה | בדיד | מקלות |
| שטח דירה | רציף | היסטוגרמה |
| מפלגה פוליטית | בדיד | מקלות |
| הסיכוי לפרוץ מלחמה | רציף | היסטוגרמה |