שחזור מבחני סטטיסטיקה

חזרה לאתר החומרים

 

שחזורים בסטטיסטיקה סמסטר א' מועד א' 2012

קצת שאלות פרקטיות  שלא מתייחסות לגרפים ותרשימים

 

1. הטווח הבין רבעוני  של התפלגות הציונים באוניברסיטה  הוא 74-85.

באוניברסיטה הוחלט להוריד 5 נקודות לאלו שקיבלו את הציון הגבוהה ביותר, ולהעלות 5 נקודות לאלו שקיבלו את הציון הנמוך ביותר. איך זה ישפיע  על הממוצע?

א. יגדל

ב. יקטן

ג. לא ישתנה 

ד. לא ניתן לדעת 

 

2. הטווח הבין רבעוני  של התפלגות הציונים באוניברסיטה  הוא 74-85.

באוניברסיטה הוחלט להוריד 5 נקודות לאלו שקיבלו את הציון הגבוהה ביותר, ולהעלות 5 נקודות לאלו שקיבלו את הציון הנמוך ביותר. איך זה ישפיע  על הטווח הבין רבעוני?

א. יגדל

ב.יקטן

ג. לא ישתנה 

ד. לא ניתן לדעת

 

3. מירי נמצאת בציון  תקן 2, יואל נמצא באחוזון ה-50, שרי נכשלה במבחן. 

לפי נתונים אלו, דרגו את התלמידים מהגבוה לנמוך.

א. שרי, יואל, מירי.

ב. מירי, שירי, יואל.

ג. מירי, יואל, שרי.

ד. לא ניתן לדעת.

 

4. בכיתה 450 תלמידים שהגובה שלהם מתפלג נורמלי. הממוצע 60, סטיית תקן 5.

כמה אחוזים גובהם מתחת ל55?

א. 50

ב.16

ג.2

ד.34

 

5. כדי לחשב סטיית  תקן, משתמשים במדד המרכז הבא: 

א. חציון 

ב. שכיח

ג. טווח

ד. ממוצע 

 

6. אם כל ערכי המשתנה  באותה שכיחות:

א. ההתפלגות היא א-סימטרית 

ב. יש הטרוגניות רבה.

ג. הממוצע שווה לסטיית התקן

ד. סטיית התקן  שווה לאפס.

 

7. במשתנה גיל הכפילו  את כל הנתונים פי 2

סטיית התקן:

א. לא תשתנה 

ב. תגדל.

ג. תקטן

ד. לא ניתן לדעת

 

8. התפלגות נורמלית  בכיתה, יעל קיבלה את הציון  55, נמצאת באחוזון ה-20.

יואל, קיבל 75 עם ציון תקן 1. מי קיבל ציון טוב יותר ?

א. יעל 

ב. יואל

ג. שניהם אותו דבר 

ד. לא ניתן להשוות.

 

9. לרונן ציון 90 בסטטיסטיקה  כאשר הממוצע הכיתתי הוא 80. ציון  התקן שלו 1.

לסמדר ציון 86 באנגלית  כאשר הממוצע הכיתתי 80, ציון תקן 2.

הציון של מי טוב יותר?

א. סמדר

ב. רונן

ג. שניהם 

ד. אי אפשר לדעת

 

10. בבית מרקחת יש  חיסונים נגד שפעת,

חיסון קשה, חיסון בינוני, חיסון קל.

על איזה סולם מדידה  ניתן למדוד:

א. סדר 

ב. מנה 

ג. רווח

ד. שמי 

 

11. דוגמא למשתנה מסג  סדר הוא: 

א. גובה התינוקות החדשים שנולדו בבית חולים.

ב. ימות השבוע 

ג. הטמפרטורה בתאילנד 

ד. מספר העפרונות בקלמר 

 

דיאגרמות 

12. ע"פ התרשים, המשתנה EDU מוגדר כ :

0 – 10 שנות לימוד – השכלה נמוכה

10-14 שנות לימוד - השכלה  בינונית 

14+  שנות לימוד  – השכלה גבוהה

לפי הנ"ל – המשתנה EDU הוא משתנה:

א. רווח

ב. שמי 

ג. סודר

ד. מנה 

 

13. מהי סטיית התקן  של המשתנה מגדר?

א. 1.2

ב. 3.6

ג. אין תשובה נכונה 

ד. 3.2

 

14. Your browser may not support display of this image. התרשים הבא מתאר התפלגות מוצא אתני, מה השכיח ביותר ?

א. WHITE

ב. BLACK

ג. SPANISH

ד.  BULGARI

 

15.Your browser may not support display of this image. לפי התרשים, מראה על התפלגות העובדים במחלקות שונות. באיזה סולם מדידה ניתן למדוד?

א. שמי 

ב. סודר

ג. מנה 

ד. רווח 

 

16. מהי השכיחות המצטברת  של השפה הTALOGIT ? (ע"פ התרשים)

א. 2.1

ב.2.4

ג. 50%

ד. אף תשובה אינה נכונה 

 

17. מתוך מאמרם של........(חפירות) שאלו את האנשים איך אתה מגדיר  את מצבך הבריאותי: 3- טוב מאוד 2- טוב 1- רע.

מהו סולם המדידה:

1. סדר

2. שמי

3. מנה

4. רווח

 

18. הממוצע בהתפלגות  נורמלית הוא 80 וסטיית התקן 10. לכן  הציון הנמוך ביותר הוא:

1. בסביבות 0.

2. בסביבות ה60

3. לא ניתן לדעת.

4. בסביבות ה50

 

19. כמה אנשים היו  סה"כ במדגם ע"פ התרשים. (היה צריך להסתכל על הTOTAL)

20. כמה אנשים ענו שהם בין 1-5 בארץ. (היה צריך להסתכל על השכיחות שלהם..)

21. מהו שיעור האנשים  שענו שפחות משנה בארץ. (היה צריך להסתכל על הValid Percent)

22. מה המשקל הכי נמוך ע"פ התרשים (מסתכלים על הטבלה...49....)

 

23. ע"פ התרשים. יש 64 שיחות שחולקו לפי מס' דק' שיחה. מה ניתן להגיד:

1. הממוצע גדול מהחציון.

2. הממוצע קטן מהחציון.

3. הממוצע והחציון  שווים.

4. אין תשובה נכונה.

מבחן בסטטיסטיקה - 2011

בבית הספר של ירדנה התפלגות הגילאים היא עם זנב ימני, ירדנה נמצאת באחוזון ה85,

ניתן להסיק ש:

א. הגיל של ירדנה הוא השכיח ביותר בבית הספר.

ב. הגיל של ירדנה גבוה מהממוצע בבית הספר.

ג. הגיל של ירדנה הוא בדיוק כמו הממוצע בבית הספר.

ד. אף תשובה לא נכונה. 

המשתנה מין (זכר-נקבה) הינו:

א. משתנה שמי בדיד.

ב. משתנה שמי רציף.

ג. משתנה רווח רציף.

ד. משתנה סדר רציף. 

רמת הכנסה נמדדת על פי סולם:

א. סודר.

ב. רווח.

ג. מנה.

ד. לא ניתן לדעת. 

בכיתה בת 20 תלמיד הוסיפו 5 נקודות ל15% מהנבחנים בעלי הציונים הגבוהים ביותר,כתוצאה מכך:

א. הממוצע ירד והשונות לא השתנתה.

ב. הממוצע גדל והשונות עלתה.

ג. הממוצע גדל והשונות לא השתנתה.

ד. הממוצע ירד והשונות עלתה. 

על איזה גרף ניתן להציג את התפלגות הנתונים מין (זכר/נקבה)?

א. היסטוגרם.

ב. עוגה.

ג. פוליגון.

ד. כל התשובות נכונות.

מבחן בסטטיסטיקה סמסטר ב' התש"ע - 2010 - מועד א

מבחן בסטטיסטיקה סמסטר ב' התשס”ט -2009- מועד ב'/ אבי גלבוע

התשובות הנכונות מודגשות.

מדי פעם הוספתי הערות משלי בצבע אדום.

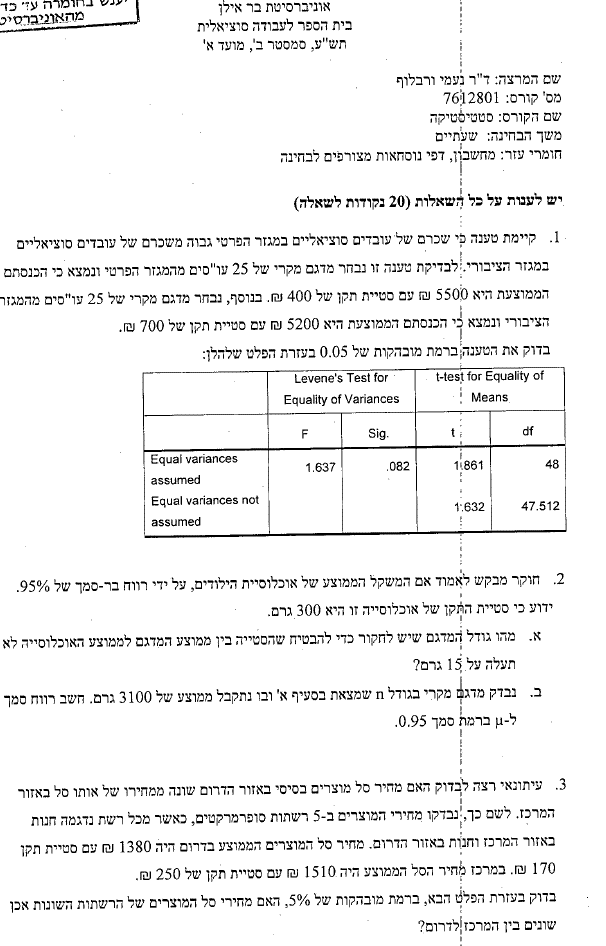
שאלה מספר 1

במחקר בדקו את גילם של הנבדקים ומיינו אותם לארבע קבוצות: צעירים (0-20), בוגרים (21-40), מבוגרים (41-65) וקשישים (66 ומעלה). משתנה הגיל הוא:

  1. משתנה תלוי.
  2. משתנה בלתי תלוי.
  3. משתנה סדר.
  4. משתנה רווח.
  5. משתנה שמי.

שאלה מספר 2

לסדרת מספרים חישבו ממוצע=200 וסטיית תקן=20.

לכל אחד מהמספרים הוסיפו 20. לאחר מכן הוסיפו 30%.

הממוצע החדש יהיה:

  1. 286
  2. 250
  3. 260
  4. 1300

שאלה מספר 3

לסדרת מספרים חישבו ממוצע=200 וסטיית תקן=20.

לכל אחד מהמספרים הוסיפו 20. לאחר מכן הוסיפו 30%.

השונות החדשה תהייה:

  1. 52
  2. 26
  3. 2704
  4. 676

שאלה מספר 4

בקבוצה של 2000 איש נמדדה ההכנסה החודשים ונמצא שהרבעון הראשון Q1=3000, הרבעון השני Q2=5500, והרבעון השלישי Q3=6500. (כל סכומי המשכורת הם לא רלוונטיים ונועדו לבלבל)

כמה אנשים נמצאים בין הרבעון הראשון (Q1) לרבעון השלישי (Q3) ?

  1. 3500
  2. 3000
  3. אי אפשר לדעת.
  4. 1000

שאלה מספר 5

בתהליך בדיקת השערות דחו את H0 ברמת מובהקות של 0.05. מכאן שניתק להסיק ש:

  1. בוודאות דוחים H0 ברמת מובהקות של 0.01.
  2. בוודאות מקבלים H0 גם ברמת מובהקות של 0.01.
  3. אי אפשר לדעת ללא חישוב או הצצה בטבלה.

שאלה מספר 6

[התייחס לנספח מספר 1] מה הממוצע של הידע הכללי?

  1. 17.95
  2. 7.78
  3. 14.83
  4. 75.4

שאלה מספר 7

[התייחס לנספח מספר 1] מה סטיית התקן של הידע הכללי?

  1. 7.78
  2. 75.4
  3. 17.95
  4. 14.83

שאלה מספר 8

[התייחס לנספח מספר 1] שאול קיבל 80 בידע הכללי. מה מצבו היחסי בציוני תקן?

  1. 0.31
  2. אי אפשר לדעת.
  3. 75.4
  4. 14.83

שאלה מספר 9

[התייחס לנספח מספר 2] שאול קיבל 12 ביצירתיות. מה מצבו היחסי בציוני תקן?

  1. 0.41
  2. 4.12
  3. אי אפשר לדעת.
  4. 0.099

שאלה מספר 10

[התייחס לנספחים 1 ו-2] באיזה מהמדדים (ידע כללי ויצירתיות) מצבו של שאול טוב יותר?

  1. יצירתיות.
  2. ידע כללי.
  3. אי אפשר להשוות ביניהם.
  4. מצבו היחסי דומה בשני המדדים.

שאלה מספר 11

[התייחס לנספח מספר 1] מירי קיבלה 72 בידע הכללי. מה מצבה היחסי בדרוג אחוזוני?

  1. 37.6%
  2. 37.6
  3. 34
  4. 34%
  5. א אפשר לדעת.

שאלה מספר 12

[התייחס לנספח מספר 2] מירי קיבלה 14 ביצירתיות. מה מצבה היחסי בדרוג אחוזוני?

  1. 71.7%
  2. 71.7
  3. 64%
  4. 64
  5. אי אפשר לדעת.

שאלה מספר 13

[התייחס לנספחים 1 ו-2] באיזה מהמדדים (ידע כללי ויצירתיות) מצבה של מירי טוב יותר?

  1. יצירתיות.
  2. ידע כללי.
  3. אי אפשר להשוות ביניהם.
  4. מצבה היחסי דומה בשני המדדים.

שאלה מספר 14

איזו תצוגה גרפית מתאימה ביותר כדי להציג את המשתנה ידע כללי?

  1. עוגה.
  2. דיאגרמת מקלות.
  3. היסטוגרמה.
  4. פוליגון.
  5. ג+ד.

שאלה מספר 15

[התייחס לנספח מספר 3] רצו לבדוק אם יש קשר בין ידע כללי ליצירתיות. בדוק זאת לגבי הנבדקים הצעירים בלבד.

  1. 0.11
  2. 0.5
  3. 0.77
  4. 0.1-

שאלה מספר 16

[התייחס לנספח מספר 3] מה מידת היצירתיות המנובאת לאדם שקיבל 70 בידע כללי? השיפוע (b) בשאלה זו הוא:

  1. 2.60
  2. 2.60-
  3. 0.23
  4. 0.23-

שאלה מספר 17

[התייחס לנספח מספר 3] מה מידת היצירתיות המנובאת לאדם שקיבל 70 בידע כללי? נקודת החיתוך של קו הרגרסיה (a) בשאלה זו היא:

  1. 69.80
  2. 69.80-
  3. 3.47
  4. 3.47-

שאלה מספר 18

[התייחס לנספח מספר 3] מה מידת היצירתיות המנובאת לאדם שקיבל 70 בידע כללי?

  1. 10
  2. 9
  3. 112.2
  4. 12.63

שאלה מספר 19

[התייחס לנספח מספר 3] מהי מידת השונות המשותפת (הכוונה לשונות המוסברת) שבין משתנה היצירתיות ומשתנה הידע הכללי?

  1. 40.7%
  2. 77%
  3. 23%
  4. 59.29%

שאלה מספר 20

[התייחס לנספח מספר 4] בדוק אם מידת הרווחה הנפשית של ניצולי השואה לפני קבוצת התמיכה הייתה שונה (שימו לב! “שונה” זה דו כיווני) מזו הקיימת אצל כלל הניצולים בארץ (ממוצע= 6.2).

כדי לפתור שאלה זו יש להשתמש ב:

  1. בדיקת השערות על הפרמטר מיו כאשר סיגמא לא ידועה. (כלומר- התפלגות t)
  2. בדיקת השערות על הפרמטר מיו כאשר סיגמא ידועה.
  3. רווח בר סמך כאשר סיגמא לא ידועה.
  4. רווח בר סמך כאשר סיגמא ידועה.

שאלה מספר 21

ערכו של ti/zi בשאלה זו הוא:

  1. 0.91 (לי יצא 0.916, כעקרון אמורים לעגל ל 0.92 אבל זו התשובה הכי קרובה)
  2. 0.94
  3. 0.33
  4. 1.41

שאלה מספר 22

ערכו של tc/zc בשאלה זו הוא:

  1. 2.131
  2. 1.96
  3. 1.761
  4. 2.145

שאלה מספר 23

החלטת החוקר בשאלה זו היא:

  1. לקבל את H0.
  2. לקבל את H0. (בטעות היו במבחן 2 תשובות זהות, שתיהן נכונות)
  3. לדחות את אלפא.
  4. לדחות את ביתא.

שאלה מספר 24

מסקנת החוקר בשאלה זו היא:

  1. הבריאות הנפשית של קבוצת התמיכה לא הייתה שונה מן הבריאות הנפשית באוכלוסיית ניצולי השואה אך יש סבירות של 0.05 לטעות מסוג ראשון.
  2. הבריאות הנפשית של קבוצת התמיכה לא הייתה שונה מן הבריאות הנפשית באוכלוסיית ניצולי השואה אך יש סבירות של ביתא לטעות מסוג שני.
  3. הבריאות הנפשית של קבוצת התמיכה הייתה גבוהה מן הבריאות הנפשית באוכלוסיית ניצולי השואה אך יש סבירות של ביתא לטעות מסוג שני.
  4. הבריאות הנפשית של קבוצת התמיכה הייתה גבוהה מן הבריאות הנפשית באוכלוסיית ניצולי השואה אך יש סבירות של 0.05 לטעות מסוג ראשון.

שאלה מספר 25

הבריאות הנפשית של קבוצת התמיכה הייתה גבוהה מן הבריאות הנפשית באוכלוסיית ניצולי השואה אך יש סבירות של 0.05 לטעות מסוג ראשון. (במילים אחרות: דחינו את H0. אגב, זאת בדיוק אותה שאלה כמו שאלה 5, אבל יותר מסובכת)

אילו בשאלה הקודמת (הכוונה למה שכתוב בשורה כאן מעל, הניסוח הזה מבלבל) הייתה רמת מובהקות 0.01:

  1. בוודאות היו דוחים H0.
  2. בוודאות היו מקבלים H0.
  3. אי אפשר לדעת ללא חישוב או הצצה בטבלה.

נספחים

נספח 1- ציונים בידע כללי

להלן טבלה ובה ציונים ממבחן “ידע כללי” שבו הציון יכול לנוע בין 40 (אין ידע כללי) ל- 100 (ידע כללי עשיר).

ציון F(x)
40-50 6
50-60 14
60-70 14
70-80 18
80-90 32
90-100 16
100


נספח 2- ציונים ביצירתיות

להלן טבלה ובה ציונים ממבחן פסיכולוגי הבודק עד כמה אדם יצירתי, שבו הציון יכול לנוע מ- 1 (בכלל לא יצירתי) עד 20 (יצירתי מאוד).

ציון F(x)
1-5 9
5-10 15
10-15 50
15-18 10
18-20 6
90


נספח 3- התפלגות ידע כללי ויצירתיות על פי גיל

(כאן למשל- ממש לא מעניין אותי המבוגרים, הוא בכלל לא שאל על זה במבחן, זה נועד רק לבלבל)

גיל ידע כללי יצירתיות
1 צעיר 78 15
2 צעיר 68 9
3 צעיר 59 10
4 צעיר 88 16
5 צעיר 63 13
6 צעיר 75 13
7 צעיר 79 17
8 מבוגר 78 13
9 מבוגר 85 12
10 מבוגר 88 9
11 מבוגר 79 7
12 מבוגר 90 10


נספח 4

בניסיון לשפר את הבריאות הנפשית אצל ניצולי שואה הציעו קבוצת תמיכה בת 12 פגישות (מספר הפגישות- פרט לא חשוב שיכול לבלבל). לקבוצה הגיעו 15 משתתפים. לפני הפגישות הם מילאו שאלון הבוחן את מידת הרווחה הנפשית שלהם (בסקאלה של 1 עד 10: ככל שהציון גבוה- הרווחה הנפשית יותר טובה). מיד עם תום הפגישות מילאו המשתתפים בשנית את אותו שאלון.

(וכאן למשל- ממש לא מעניינת אותי העמודה השמאלית, כלומר מה קורה “אחרי”, הוא בכלל לא שאל על זה במבחן, זה נועד רק לבלבל)

רווחה נפשית לפני רווחה נפשית אחרי
1 7 8
2 8 8
3 5 6
4 6 5
5 4 8
6 5 8
7 8 7
8 7 9
9 6 8
10 5 5
11 6 6
12 7 8
13 8 8
14 9 9
15 7 9

שחזור מבחן בסטטיסטיקה- 76-128-01- ד”ר אבי גלבוע

שנה א'- התשס”ט- סמסטר ב' מועד א'.

שאלה מספר 1

לסדרת מספרים חישבו ממוצע= 400 ושונות= 29 לכל אחד מהמספרים הוסיפו 100. לאחר מכן הפחיתו 20% מערכו שלח כל מספר.

הממוצע החדש יהיה:

  1. 400
  2. 480
  3. 320
  4. 600


שאלה מספר 2

לסדרת מספרים חישבו ממוצע= 400 ושונות= 29 לכל אחד מהמספרים הוסיפו 100. לאחר מכן הפחיתו 20% מערכו שלח כל מספר.

השונות החדשה תהיה:

  1. 103.2
  2. 23.2
  3. 82.56
  4. 18.56


שאלה מספר 3

לסדרת מספרים חישבו ממוצע= 400 ושונות= 29 לכל אחד מהמספרים הוסיפו 100. לאחר מכן הפחיתו 20% מערכו שלח כל מספר.

סטיית התקן החדשה תהיה:

  1. 23.2
  2. 10.3.2
  3. 25.8
  4. 4.31


שאלה מספר 4

בתהליך בדיקת השערות קיבלנו H0 ברמת מובהקות של 0.05. מכאן ניתן להסיק ש:

  1. בוודאות מקבלים את H0 גם ברמת מובהקות של 0.01
  2. בוודאות דוחים את H0 ברמת מובהקות של 0.01
  3. אי אפשר לדעת ללא חישוב או הצצה בטבלה.


שאלה מספר 5

במסגרת מחקר נבדקו 100 איש. הגובה החציוני הוא 175 ס”מ, וס.ת היא 20.

אח”כ הוסיפו 2 אנשים, אחד מהם גובהו 199 ס”מ, והאחר- 173 ס”מ.

כיצד ישפיעו על החציון החדש?

  1. יגדל.
  2. יקטן.
  3. לא ישתנה.
  4. אין מספיק נתונים כדי לדעת.

שאלה מספר 6

במסגרת מחקר נבדקו 100 איש. הממוצע הוא 178, וס.ת היא 20.

אח”כ הוסיפו 2 אנשים, אחד מהם גובהו 199 ס”מ, והאחר- 173 ס”מ.

כיצד ישפיעו על הממוצע?

  1. יגדל.
  2. יקטן.
  3. לא ישתנה.
  4. אין מספיק נתונים כדי לדעת.


שאלה מספר 7

במסגרת מחקר נבדקו 100 איש. הממוצע הוא 178, וס.ת היא 20.

אח”כ הוסיפו 2 אנשים, שגובהם גם הוא 178 ס”מ.

כיצד הדבר ישפיע על סטיית התקן?

  1. יגדל.
  2. יקטן.
  3. לא ישתנה.
  4. אין מספיק נתונים כדי לדעת.



טבלאות נספחות לשאלות הבאות (8-18):

כיתה 1
ציון f(x)
40-50 4
50-60 8
60-70 10
70-80 12
80-90 15
90-100 9
סה”כ: 58

כיתה 2
ציון f(x)
40-50 8
50-60 12
60-70 13
70-80 10
80-90 4
90-100 3
סה”כ: 50



שאלה מספר 8

מה ממוצע כיתה 1?

  1. 84.14
  2. 74.14
  3. 10.24
  4. 7.24



שאלה מספר 9

מה סטיית תקן כיתה 1?

  1. 14.89
  2. 60
  3. 3.21
  4. 15.02


שאלה מספר 10

מה ממוצע כיתה 2?

  1. 64.8
  2. 51.7
  3. 7.71
  4. 8.4


שאלה מספר 11

מה סטיית תקן כיתה 2?

  1. 14.07
  2. 13.93
  3. 10.97
  4. 3.93


שאלה מספר 12

מהו ציון התקן של אלי שקיבל 62 בכיתה 1?

  1. 0.2-
  2. 0.2+
  3. 0.82+
  4. 0.82-


שאלה מספר 13

מהו ציון התקן של רמי שקיבל 62 בכיתה 2?

  1. 0.2+
  2. 0.2-
  3. 0.6-
  4. 0.6+


שאלה מספר 14

אצל מי מהשניים (אלי ורמי) המצב היחסי טוב יותר? (בדוק לפי ציוני התקן).

  1. מצבו היחסי של רמי טוב יותר.
  2. מצבו היחסי של אלי טוב יותר.
  3. מצבם היחסי דומה.
  4. תלוי, במובנים מסוימים של אלי טוב ובמובנים אחרים של רמי טוב.


שאלה מספר 15

לרחל מכיתה 1 נודע שמצבה היחסי טוב: 83% מתלמידי הכיתה נמוכים ממנה.

מה ציונה הגולמי?

  1. 78.79
  2. 92.11
  3. 85.56
  4. 89.56

שאלה מספר 16

לשלומי מכיתה 2 נודע שמצבה היחסי טוב: 83% מתלמידי הכיתה נמוכים ממנה.

מה ציונה הגולמי?

  1. 79.6
  2. 83.1
  3. 77.0
  4. 78.5


שאלה מספר 17

מה השרטוט המתאים לתוצאות כיתה 2?

  1. דיאגרמת מקלות.
  2. עוגה.
  3. פוליגון.
  4. היסטוגרמה.
  5. 3+4 נכונות.



* כאן הייתה שאלה (שאלה מספר 18) על מדדי א- סימטריה של ספירמן, שחלה בה טעות. התשובה שהייתה הכי קרובה לתוצאה היא 0.86-

* לאחר מכן היו עוד 12 שאלות עם נספח נוסף לגבי בדיקת השערות (סה”כ 30 שאלות במבחן)- לא הספקתי להעתיק אותם.

מבחן בסטטיסטיקה – מועד א ד”ר פורטוביץ - 2008

מבחן בסטטיסטיקה – מועד א ד”ר פורטוביץ - 12/7/06

  1. להלן נתונים על 22 בנים ובנות בחמישה משתנים:
מגדר גיל דירוג פופולאריות ציון פנימייתי או אקסטרני
א בן 14 1 7 פ
ב בן 14 2 7 פ
ג בת 12 3 7 פ
ד בת 11 4 8 א
ה בן 13 5 8 א
ו בן 14 6 7 פ
ז בן 16 7 7 פ
ח בן 17 8 8 א
ט בן 15 9 9 א
י בת 14 10 6 פ
יא בת 13 11 5 פ
יב בן 12 12 5 פ
יג בן 18 13 7 א
יד בת 16 14 10 פ
טו בת 17 15 10 פ
טז בת 15 16 10 פ
יז בת 13 17 9 א
יח בת 12 18 8 א
יט בת 12 19 9 א
כ בת 14 20 10 א
כא בן 14 21 10 א
כב בן 15 22 7 א

  1. האם יש הבדל בין בנים לבנות באשר לציוניהם?
  2. הציון הממוצע בעולם של בנים הינו 7.5 עם סטיית-תקן של 1.0. האם הבנים במדגם שונים מן הממוצע העולמי?
  3. תמיד חשבתי שממוצע הציון של בנות הינו 8. האם אני צריך לשנות את עמדתי?
  4. האם יש קשר הין גיל לבין ציון?
  5. האם יש קשר בין ציון לבין פופולאריות?
  6. האם יש הבדל בין דירוג הפופולאריות של בנים לעומת דירוג הפופולאריות של בנות?
  7. האם יש הבדל בין בנים לבנות באשר לשהותם בפנימייה?
  8. להלן מידת שביעות רצונם של 40 בנים ושל 40 בנות. האם יש טעם לומר שבנים יותר שבעי רצון מבנות?
מס' הבנים מס' הבנות
שר”מ 7 4
ש”ר 8 6
בינוני 15 10
לש”ר 5 10
בלש”ר 5 10
סה”כ 40 40


1. קוביה מוטית כך שהסיכוי לקבל 4 הוא 0.4. בהטלת הקוביה פעמיים, מה הסיכוי שב-2 הפעמים תצא תוצאה ה*שונה* מ-4?
א. 36
ב. 0.16
ג. 0.30
ד. אף תשובה אינה נכונה
(התשובות לא מדוייקות, אבל התשובה היא ד', כי ההסתברות היא 0.36 לא 36 [או שיש בעיה בניסוח וזאת התשובה באחוזים, אבל לא נראה לי כי לא רשום %].

2. הטילו 3 פעמים מטבע. מה הסיכוי לקבל עץ לפחות פעמיים?
א. 0.375
ב. 0.3
ג. 0.5
ד. ?
(התשובה - ג' לפי סיכום בינום של 2 מתוך 3 ו-3 מתוך 3)

3. הסיכוי שאדם הוא סטודנט לפסיכולוגיה הוא 0.3. הסיכוי שאדם צפה אתמול בערב בטלוויזיה הוא 0.10. מה החיתוך של האירועים?
א. 0.03
ב. 0.40
ג. 0.2
ד. ?
(התשובה א)

4. יש שני משתנים שונים, בשניהם הממוצע הוא 10 וס. התקן 3. מה נכון בהכרח?
א. המתאם חיובי
ב. המתאם שלילי
ג. R=1
ד. אף אחד לא נכון בהכרח

5. במשוואה y=a+bx מתי y=a?

6. מתי (Y מנובא מינוס Y ממוצע) חלקי (Y נצפה Y ממוצע) יתן 1?
א. כש-R=1
ב. כשכל הצפיות נופלות על קו הרגרסיה.
ג. א+ב.
(מישהו מוכן לענות/לתקן?)

7. מאמן שקל את כל מתאגרפי הסומו שלו ומצא שהמשקל הממוצע הוא 156 ק”ג עם סטיית תקן של 20 ק”ג. הוא התבקש לתקן את הדו”ח : א) התברר שהוא טעה והמשקל ששקל את הסומואים הכפיל כל תוצאה ב-2. ב) ביקשו שהמשקל יוצג בגרמים.
מה היו הממוצע והס. תקן בדו”ח המתוקן?


נתון משתנה המתפלג באופן הבא: הממוצע=10 וסטיית התקן=3. מה בהכרח יהיה המתאם עם משתנה המתפלג באופן דומה (עם אותו ממוצע ואותה סטיית תקן)?
א. חיובי
ב. שלילי
ג. 1
ד. לא ניתן לדעת
ה. לא ניתן לדעת, אך קוזלובסקי צריך אשפוז

התשובה שלי- א. (התלבטתי מול ה')
אבל לאחר שהבטתי בנוסחא, נראה לי שזה יוצא 0, אז התשובה היא כנראה-לא ניתן לדעת.
הנוסחא:
סכום{(x- ממוצע) * (y-ממוצע)}


n*Sy*Sx


נתונה קובייה מזויפת בה הסיכוי לקבל מספר 4 הוא: 0.40. מהו הסיכוי לקבל פעמיים מס' שונה מ-4?
א. לא ניתן לדעת
ב. 0.60
ג. 5/36
ד. 16
ה. 36
ו. לא ניתן לדעת ונכשיל אתכם עם טעויות הדפסה

עניתי א', א ב ל :
באחת הכיתות גורית אמרה שבמקום התשובה של 36 צריך היה להיות 0.36 !!!
לכן חייבים לבקש לפסול את השאלה.

נתון ממוצע=46, ו50% קיבלו מעל 46. מה ניתן לומר?
א. יתכן שזוהי התפלגות נורמלית
ב. הממוצע גבוה מהחציון
ג. עוד משהו
ד. עוד משהו יותר מבלבל

עניתי א', אבל אח”כ הבנתי שזה כנראה ב'.
כי צריך לדייק במילים: קיבלו מעל 46”


מתי Y נצפה = Y מנובא?
א. כש r=1
ב. כשכל התצפיות נופלות על קו הניבוי
ג. א+ב
ד. לא ניתן לדעת

עניתי - ג.


נתון התפלגות נורמלית עם ממוצע=7000, ס”ת=1500.
מוסיפים 10% לכל מי שמתחת לחציון.
מה יקרה לממוצע ולחציון?
א. ממוצע-יגדל, חציון-יקטן.
ב. ממוצע-יקטן, חציון-יגדל.
ג. לא ניתן לדעת.
ד. חי לבלתי תלויים (נו, באמת, אני לא זוכר את כל המסיחים...)

תשובתי: ג'.
למה? כי זאת לא טרנספורמציה ליניארית, לא עשו את אותה פעולה על כולם. לא ברור מה יקרה.
חוצמזה- מדובר בכפל ב- 110/100, ואם ישנם ערכים שליליים הם רק יהפכו ליותר שליליים


עוד שאלה: ציון בסטט וציון במבוא מתאם 1 אם בסטט דני קיבל 100 וזה היה הציון הכי גבוה מה זה אומר על הציון במבוא?
א. גם במבוא הציון 100
ב. הוא קיבל גם במבוא את הציון הכי גבוה
ג. א+ב

1) אם P(A)=.30 , p(B)=.20, P(AandB)=.52 אזי מה שווה הסיכוי ל A וגם B (כפל) ?

א. 0.02-
ב. 0.22
ג. 0.32
ד. יש טעות בחישוב
ה. הכול לא נכון

לפי הנוסחה יוצאת תשובה א. מכיוון שזה מספר שלילי אז יש טעות בחישוב. צודק


Locations of visitors to this page